1983年 東京大学 数学（理系） 前期

12日に友達が泊りに来てマリカとマリテオールして、13日は学科の飲み会で14日はバイトの二次選考の流れでブログを書く気力おきませんでした笑

大学の勉強のほうは、微分方程式を1から独学を始めました。先輩にテキスト借りて早く終わらせるためにとりあえず頑張ります。

難しく考えずに、素直に問題文に従っていきます。

後、これは必要条件と十分条件に分けていくのが定石だと思います。一気に必要十分を考えるのが難しいからです。

(1)より、任意の形ですが、特殊な三角形を考えてみたいと思います。正三角形です。

(2)より、とりあえず、A(1,√3)、A'(-2,2√3)と置きましょう。原点は自分自身に移るので、

Bを(2,0)と置いて△OABが1次変換によってどこに行くか考えましょう。

必要条件として、2つの行列が出てきます。なぜならBの移動先の候補が二つあるからです。

十分条件を確認すると確かに題意を満たしているので大丈夫です。

二進法に気付けばほとんど自明ですね。一応帰納法です。nの値を代入していけばわかります。二進法に気付けないときは、いっきに二つの事柄を証明します。anと(1)と(2)の内容です。

題意に従って、文字を置いていきましょう。

円C上の点Pは(cosθ,sinθ,0)とおけ、(0≤θ<2π)

直線l上の点QはA(a,0,0)をとおり、xy平面とのなす角が45°なのでQ(a,t,t)とおけますね。(t∊R)

最短距離をaとθで表して、最小値を求めましょう。

1文字固定をしましょう。aの大きさ（つまりAの位置)で場合分けが生じます。

場合分けをするのは問題文に従えばすぐわかりますね。

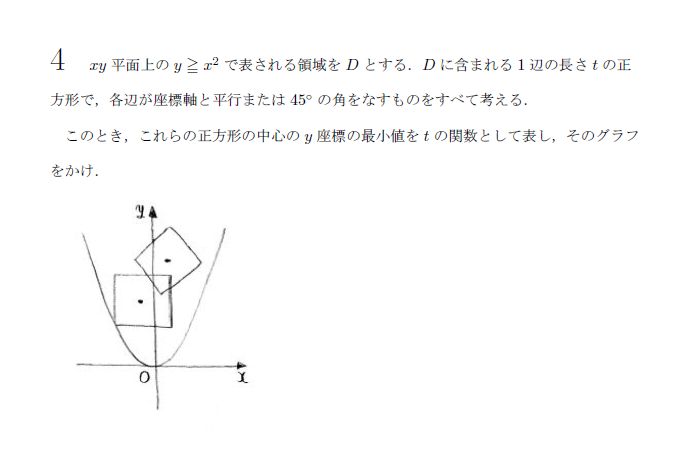
(ア)正方形の各辺が各座標軸と平行なとき、

最小値ってことは、正方形の下側の頂点2つがy=x^2に乗ってればいいですね。

下側の頂点が(±t/2,t^2/4)と表せるので、このとき、中心y座標のminが出ますね。

(イ)45°のとき、

これも２つ場合分けが生じますね。

下側の頂点が原点と一致するか、左右の頂点がy=x^2上にあるかどうかですね。

y=x^2とy=±xの交点を考えると、この２通りが同時に起こる正方形の一辺の長さは√2ですね。

その値より、大きいとき、小さいときで、考えればいいですね。

全部の場合分けが終わったらグラフを書きましょう。

minなので、そのグラフを考えたとき、yの値が大きくないほうを選べば勝ちです。

対称面の切り口を考えるのが定石ですね。長さを変数で置いてもいいですが、対称面の角度を変数にとる方が楽な気がします。

これは難しいと思います。2番か6番がこの年の踏ん張りどころでしょうか。

とりあえずy=aでぶった切ります。切り口はaを消去すると、x^2+z^2=-y+3/4です。

さて、次にHを考えますが、y=xとしてもいいでしょう。/////

そんで、y=xに平行な平面y=x+b(b≧0)で切った断面をxz平面に正射影します。

その図形は(x+1/2)^2+z^2=1-bですね。1-b≧0⇔b≦1より、この図形の面積はπ(1-b)ですね。

y=x+bとxz平面は45°の角をなすから、正射影前の図形はπ(1-b)/cos45°=√2π(1-b)です。

y=x+bとy=x+b+Δbの距離はΔb/√2であるから、体積は

∫[0→1]√2π(1-b)・db√2=π/2　が答えです。

この問題が難しいと思うポイントは

①回転体が不完全で、回転軸に垂直で切っても無理

②正射影が思いついたとして、元に戻してあげたとしても、その微小体積を足し合わせるときに厚みがΔyとかでないこと。

いわゆる斜回転体の先駆けでしょう。

別解はいくらでもあります。/////までは思いつかないといけないと思いますが…

3(10分)→4(15分)→1(15分)→5(20分)→2(30分)→6(30分)