1982年 東京大学 数学（理系） 前期

以下、太文字をベクトルとします。ベクトルOPをpとします。

題意よりAp=p⇔(A-E)p=0ですね。ここで、A-Eが逆行列をもたないと仮定しましょう。つまりdet(A-E)≠0と仮定します。そうするとp=0となりますが、点Pは原点以外に矛盾しますね。

よってdet(A-E)=0です。(a-1)(d-1)-bc=0(2点)

ここで、lは、sx+ty=1(s,t∊R\｛0｝)とおけるのは大丈夫でしょうか。s=1/m,t=1/n的に置くとx切片がm、y切片がnの直線になりますね。原点は通りません。(3点)

この直線上の点A(x,y)を一次変換で移しましょう。A'(ax+by,cx+dy)ですね。こいつが元の直線にいるにはsx+ty=1を満たす(x,y)に対してs(ax+by)+t(cx+dy)=1を満たす(s,t)が存在すればいいです。（s,tって置いたのは分数を嫌ったからです）(4点)

(a-1)s+ct=0とbs+(d-1)t=0が条件ですね。この2式の係数を並べた行列の行列式は0になっています。最初のほうに戻って確認してください。

よって、(a-1,s)と(b,d-1)は一次従属です。(3点)適当にr(≠0)とp,q∊Rを用いて

(a-1,b)=pr、(c,d-1)=qrとおけますね。よって、２式に戻して考えると、ps+qt=0を満たせばよいですね。(3点)

p≠0とすると、(s,t)=(-q,p)、p=0の時は、(s,t)=(1,0)とすれば満たされます。(4点)

以上より示されました。ポイントはlの置き方とかでしょうか。

正四面体の辺に接するんです。辺ですよ、辺。イメージし難いんじゃないでしょうか。面とかがあるからいけないんでしょうね。とっちゃってみましょう。

その辺にある爪楊枝6本もってきてくっつけると、空洞ですよね？そんな感じです。

解法は2つありますよね。対称面で切る方法(定石)と正四面体と立方体の関係です。

 体積は、結局回転体の体積として扱いますけど、対称面は見つけてもらうとして、正四面体と立方体の関係を考えます。

立方体の頂点から4点をうまくもってくると、正四面体が得られます。確かめてください。そうすると、立方体の球面Sの内接球っていうのは、各面の中心で接しているから、Tの各辺は立方体の対角線となってますよね。よって、立方体の1辺の長さは2なので、答えは2√2です。前半終了です。(10点)

後半は、積分です。

Tの1つの面の内接円の半径は、√(2/3)です。これは頂点から底面におろした垂線の足は底面の重心になることからですね。(2点)

ぼこっと出ている題意の体積部分までの球の中心からの距離は、√3/3です。計算してみてください。これが4つあります。積分して終了です。(8点)

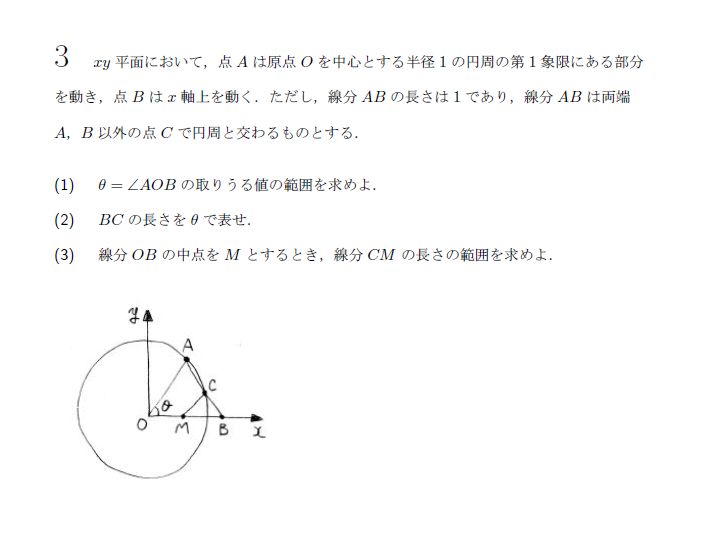
(1)ABと円がA,B以外の交点をもてばいいですね。(5点)

(2)計算です。△OABは二等辺ですから、解けますね。(5点)

(3)△BCMに着目しましょう。余弦が使えます。

CMの２乗を計算できたら、グラフ等を利用して範囲を出しましょう。(10点)

これは物理やっている人はできますね。波動的な。

x方向、y方向に分けて議論しましょう。答えはV^2ですね。

非回転体の体積ですね。概形は１式が竹を斧でぶった切って出てくる、ぐわんとなったやつです笑　ごめんなさいまったく概形考えなくていいですよ笑

どの文字で切るかは、わかりますか。xかyです。式に出てきた回数または高次のもので切りたいからです。とりあえずy=tで切りたいですね。(0≤t≤1)

切り口は台形ですね。面積を求めます。

これを0から1まで積分して終了です。

(1)計算しましょう。(2点)

(2)推移図を考えましょう。(6点)

(3)pn+qn+rn=1が成り立つことを気づくと(2)の結果から瞬殺です。(12点)

3(15分)→5(10分)→6(15分)→4(25分)→2(20分)→1(15分)

書いているときに思いました。重いです笑

だから、まぁ簡単だなってやつはものすごく簡略してます。別に適当にしてるわけじゃないですよ汗