1984年東京大学数学（理系）前期

空間座標の方程式を知らないときついです。

Cの周はCを含む平面と中心(0,1/√2,1/√2)、半径1の球面との交わりです。

Cを含む平面は、y-z=0と考えられます。この平面は(1,0,0)と(0,1,1)に平行であるから、(0,1,-1)を法線ベクトルとしてもつからです。また、今回の球面は

x^2+(y-1/√2)^2+(z-1/√2)=1と書けます。

ⅰ)とりあえず、Sの輪郭上の点をQ(a,b,0)とします。直線PQ上のある点Rは

(ta,tb,2√2(1-t))と表せますね。(t∊R)

この点Rがy-z=0上にあるときは、tをa,bで表せますね。これでRの座標がすべてa,bで表せますね。

これを球面の式に代入しましょう。整理すると、円の式が出てきます。

ⅱ)

幾何的に解きましょう。大きい円錐と小さい円錐を見つけたら終了。

２つの曲線が接していて、共通の接線が引けることに注目しましょう。

三平方の定理や直交する条件を使いましょう。

難しくはないと思います。

難しいですね…。頭の柔らかさ？がキーポイントだと思います。

ⅰ)Σ[k=2→n]akfk(x)と表されることは、理解できると思います。

a0=a1=0となれば終了です。

ポイントとしてはfk(x)が(x-a)^kで割り切れるとはf(a)=f'(a)=0=…f^(k)(a)=0が成り立つこと。TeXの表し方で表せるようになったらこの部分はわかりやすくしようと思うので…。これを使いましょう。

ⅱ)　ⅰ)を使いましょう。ⅰ）の条件に加えてg''(1)=0が成り立ちますね。

回転させる前に軸に平行なものでぶった切ります。切り口はドーナッツの形になりますね。その面積を求めて、積分しましょう。

方針はすぐに立つと思いますが、計算量は非常に多いと思います。直接確率を出すか、確率漸化式の方法がありますが、後者のほうがほんのちょっと楽かと。

計算量で思い出しましたが、数学科の専門授業でそれぞれの分野に対し演習の授業がうちの大学にはあります。（これだけで特定されてしまう可能性も否めませんが笑）

各担当の教授によってその演習の方式はガラッと変わりますが、ある分野の演習の担当として数学科の中で一番厳しいと言われている先生に僕の学年は後期に当たっていました。黒板の前で発表の形式ですが、非常に寧な方で、少しでも計算過程を省くと容赦なく突っ込んでくるのでプレッシャーとの戦いでした。（僕は３回発表しましたが笑）頭の中で計算してしまうので、何回か厳しめに指導されて少し心が折れましたが、毎週の宿題を解いているうちに計算力は非常に上がったと思っています。東大の問題を俯瞰しても、計算がややこしいものでも、嫌がることはなくなったのでとても感謝しています。笑　高校の時にこういう先生に出会いたかったｗ

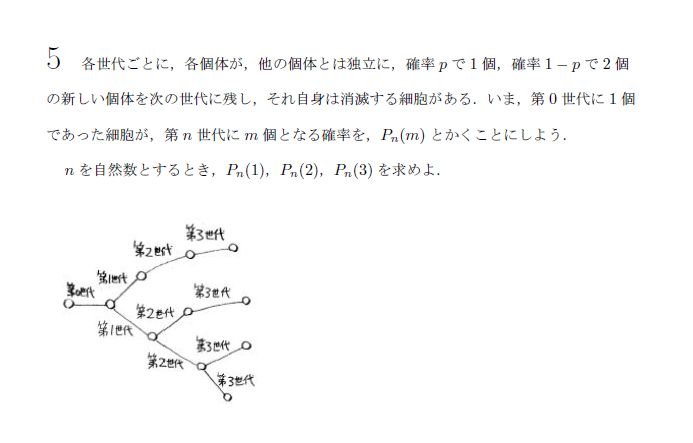
閑話休題、とりあえず、推移図を書きましょう。個体数が減少することはないことをうまく考えましょう。

Pn(1),Pn(2)は計算量としてはそんなに多くないです。

また、Pn(2)、Pn(3)は、場合分けが生じます。頑張りましょう。