1981年 東京大学 数学(理系) 前期

前半のほうは楽ですが、後半がかなり難しいです。
(前半)ようは、一度選んだやつを永久的に選ばなければいいですね。
(ア)n<2kのとき、k回取り出さないといけないのに、少なくとも一つの要素は必ずダブってしまいますよね。よって、このときは0通りです。(2点)
(イ)n≧2kのとき、ダブりを生じないようにすればいいんです。
nC2・n-2C2・…・n-2(k-1)C2/k!ですね。分子は選ぶ順番を区別しているから、k!で割りましょう。(3+3点)
f(n,k)=n!/(2^k・k!(n-2k)!) (n≧2k),0(n<2k)です。(2点)
(後半)f(n,k)=f(n,1)を考えます。整数問題なので、整数特有の考え方(範囲絞りや、約数や倍数など)を引っ張り出してきましょう。でも、難しいです。
とりあえず、f(n,k)=f(n,1)を計算しましょう。
(n-2)!/(n-2k)! =2^k-1・k!∧n≧2kです。
で、ここが思いつくのに苦労するのですが、両辺を(2k-2)!で割ります。
そうすると、左辺がn-2Cn-2kになります。そうです。整数になるんです。
右辺はk/(2k-3)(2k-5)・…・3・1となります。こいつも整数にならないと等号成立しません。(3点)
k≧2k-3っていうのが必要になります。k=2,3ですね。場合分けを始めましょう。(3点)
(a)k=2のとき、
n^2-5n+2=0となりますが、これを満たすn∊Nはいないですよね。(2点)
(b)k=3のとき、
n-2C4=1ですね、これは、代入してみるとわかりますが、n=6のとき題意を満たしますね。(2点)
よって答えは(k,n)=(3,6)です。お疲れ様でした。

無作為にしてもいいですが、とりあえず、A1を最初に選ぶとしても一般性失いませんね。(3点)
三角形の種類は、面積0、√3/4(連続する3点)、√3/2(直角三角形),3√3/4(正三角形)の4種類です。(5点)
A1で固定しているので、残りの選び方は36通りで同様に確からしいです。(3点)
36通りなのだから、さいころの時に書くグラフを書いて、どの時がどの三角形かを書いちゃいましょう。(5点)
期待値出して終了(4点)

順像法、逆像法が思い浮かびますね。ですが、逆像は計算量多くなりそうなので、順像法を選びましょう。
y'=2xより、点Qでの法線ベクトルの一つは、(2t,-1)です。これを正規化(大きさを1に)しましょう。(2点)
(ハ)の条件を求めると、複号同順として、二つの点が出てきます。(3点)
場合分けすると、一つのほうは(ロ)を満たさないので、結果1つのみになります。 (3点)
もう一つの点はparameterのtを消すとx=y-2y^2+2y^3上に存在することがわかります。
yについて微分すると、単調増加していることがわかります。0≦t≦1の下では、y^2y^2+2y^3≦√yになっています。これを示すことで(ロ)を満たしていることが言えますね。(3点)
グラフを書いてみましょう。点Pの書く曲線は、C'の0≦y≦1としてよいですね。(3+2点)
積分しましょう。終了です。(4点)

図形的に解く方法と、計算をするだけの方法が思い浮かびますね。
僕個人のこの問題に関する考えとしては、理系の子に関しては図形的に解いた方がいいと思います。ですが、まだ、ブログに図の上手な乗せ方を知らない僕にとって、図形的解法を乗せるのは難しいので、計算方法で解きます。ごめんなさいorz
とりあえず、以下太文字をベクトル表記します。
L=(0,0,1)とします。これはz軸に平行な直線の方向ベクトルです。
(ロ)について、ベクトルPA・L=|ベクトルPA||L|cosπ/4をx,y,zで表します。
(イ)より両辺正なので、2乗しても同値性は崩れません。2乗して、整理します。
これを、(ハ)、(ニ)についても同じような作業をします。(1+1+1点)
(ロ)(ハ)(ニ)から出てきた式をそれぞれ1,2,3とします。
1-2より、y=0…④がでてきます。(理系の子はここで、xz平面上にPは存在すると気づきましょう。)
y=0を残りに代入すると、
z^2=(x-1)^2+1と、x^2=(tanα)^2が出てきます。後者で、x=±ztanαと出てくるので前者に代入しましょう。
((tanα)^2 -1)z^2∓2ztanα+2=0…★が出てきます。
zの方程式の正の実数解を考えていきます。(5点)
(ア)(tanα)^2=1⇔α=π/4のとき、z=1です。よって、対応するPは1つですね。
(イ)α≠π/4のとき、★の判別式は2-(tanα)^2です。つまり、
0≦tanα≦√2のときは実解をもちますね。√2<tanαだと、もちません。(3点)
後は、(tanα)^2 -1の正負で場合分けしましょう。KKKを用います。(3+3点)
よって、答えは、5つ出てきます。(複合同順で表すと、3つになります。)(3点)

半径1を上手に使いましょう。長さと角度どちらを変数と置くかは自由ですが、長さのほうがいいでしょうか。条件として長さがもらえているので。置いたときに変数の範囲はチェックしましょう。
これは、方針言わなくても解いたほうがいいですね。ただ、体積が出て、すぐに微分すると、今回は重いです。変数部分だけを微分するってことも念頭に入れておきましょう。(1)で12点、(2)で8点くらいでしょうか。

(1)イとロから、c,dを消すことができます。f(x)=ax^2+bx^2-ax-b=(ax+b)(x^2-1)です。
次はハです。x=±1のときは、(ハ)は常に成立します。
|x|<1の時は、x^2-1<0より、ax+b≦(1-|x| )/x^2-1 ですね。両辺のグラフを考えましょう。4つの条件式が出てきます(10点)
(2)積分しましょう。a,bの式が出てきます。bとかをfixするとa=0のときにminになります。moveさせるとb=-1のときにminとなります。以上より、f(x)=1-x^2です。(10点)
更新前回より遅くなってすいませんでした!昨日新宿のバーで友達と飲んでいたせいで今日一日がスローライフでした汗
リンク先に貼ってあるブログを書いているじゅかさまとカフェで数学の話とかをしていたので…
とたけけが前年度の問題を解いてくれたこともあってか、しれっと80年代に入りましたね。おそらくここからは難しくなっていくんでしょう。
前年度第2問のように、深く考えていこうっていうスタンスで解説しようと思う問題が出て来たらその問題を1つの記事として書いていこうかなと思っています。
東大数学を考える。①

Descartesの言葉通り、分割していきましょう。
「長さ2の線分NSを直径とする球面Kがある。」
NSっていうから地球を想像してしまいますよね。笑
いっそのこと地球で考えましょう。
「点Sにおいて球面Kに接する平面の上で、Sを中心とする半径2の四分円ABと線分ABを合わせて得られる曲線上を、点Pが1周する。」
つまり、南極点での地球の接平面っていうように考えましょう。
人間の目は、勝手に地球を平面のように感じるようにできてます。たぶん。
自分の目から長さ2(つまり、地球の直径分)のところに問題文のようなA,Bがある感じですね。分度器みたいな形の(全然半円じゃないけど)部分をぐるぐるします。
まずは、落ち着きましょう。
SS(方針)がつかめるは手を動かすことも(計算)大事だけど、図を考察することも大事だということを感じましょう。
この問題は、解法の選択ミスで、まったく解けなくなると思います。この問題に初めて出会った僕のように…笑
とりあえず、四分円ABと線分ABを動くのだから、1つずつ考えることにします。
(ア)Pが線分ABを動くとき
このときは、A,B,P,Nは同一平面上にずっといますね。ってことは,
Qの軌跡はKと平面NABの交線になりますね。
イメージ的に考えると、Qの軌跡は赤道の一部分とでも考えてみてください。。
球面から平面による切り口は円になります。△NA'B'の外接円です。
NA',NB',A'B'の長さはそれぞれの点と球の中心Oを結んだ三角形を考えると√2とわかります。
正弦定理より、△NA'B'の半径は√6/3ですね。
点Qの描く曲線の長さはこの外接円の1/3です。2π・√6/3・1/3=2√6π/9…(ⅰ)
(イ)Pが弧ABを動くとき、
動かしていればわかりますが、NP:NQは2:1で一定ですよね。相似を使ってみましょう。軌跡は半径1の四分円です。 π/2…(ⅱ)
(ⅰ)+(ⅱ)より、答えは(9+4√6)π/18です!
(イ)のほうは、やっていませんが、(ア)のほうは空間図形を断面で考えています。平面に落とすことをちゃんとやってします。
閃きが必要となると思います。前記事にも書いたように、この問題は最後に解くとして、体力も気力も奪われた状況下で、根気強く考えていかないといけないです。
こういう問題こそ東大らしいって言ってもいいと思います。もちろん今までの問題の中にも東大らしさはあったのですが笑
1980年 東京大学 数学(理系) 前期
テスト終わって、やっと春休みが来ました笑
この年は同じ学科のとたけけ君(以下、犬)に解いてもらいました。
でも、さすがに大学数学に漬かっている彼に対策なしで解かせるのも酷なので、わからなさそうな問題ヒントを少しだけ出してあげました。
(犬:25分)(与えたヒント:Menelaus th.)
(1)BQを余弦定理とかで出します。
根号の中身が正であることをちゃんと確認しましょう。(2点)
Menelausで、BB'と、PB'を出しましょう。(5+5点)
(2)△A'B'C'が正三角形であることを証明しましょう。
相似等を駆使して、角度がすべて60°であることを証明。
△A'B'C'の面積は√3/8になりますね。
1辺の長さを求めます。(2点)面積を出して比較しましょう。(3点)
2次方程式が得られます。解いてx<1/2を考えて答えを出しましょう。(3点)

気づけばあ~ってなります。僕は浪人の初めごろこの問題に出会い、全然わからなくて泣いた覚えがあります。それを思い出させる懐かしい問題でした。
(犬:give up)
この問題は、次の投稿に1つ丸ごと解説したいと思います。

(犬:20分)
(1)これは線形代数Ⅱに触れている彼にとっては容易だったようです。
Aの各成分から√2をくくりだすとπ/4回転行列になりますね。
回転行列のn乗はcosやsinの中身がn倍になることはわかりますか?帰納的にわかります。A^nを計算しましょう。(4点)
pnとqnを出しましょう。(1点)
qn=0より、(cosnπ/4,sinnπ/4)と、(1,α)が直交すればいいですね。αの答えは3つです。(5点)
(2)
anを、表しましょう。
mod4で場合分けして考えましょう。αの式が出てきます。(4×1点)
これらが一致することはあり得ないのですが、その証明は、
α=xとして、y=f(x)のグラフを書いてみるのがいいと思います。(3+3点)

(犬:10分)
素直にx^2+y^2を計算しましょう。sintcostは倍角で直しましょう(5点)
k∊R+なので、tについての微分をしましょう。極値が出てきます。(5点)
ここでポイントなのは、sin2tには範囲があることです。|sin2t|≦1です。
極値が区間にいるか否かで場合分けします。(5+5点)

(犬:15分)
(1)帰納法です。k秒後に、題意が成り立つと仮定してk+1秒後も同じだよって示しましょう。(10点)
(2)帰納法の議論で出てきた漸化式を解くだけです。p1(n)から出しましょう。(5+5点)

(犬 give up)(ヒント:三角形大きくなるとxy=1と交わるね。)
これは…解いてほしかった。
とりあえず、点A(a,b)と置きます(a>0,b>0) 面積s=abとなりますね。(2点)
abの値がどんなときに、xy≦1と交点を持つのか、持たないのか。その場合分けをしましょう。(6+6点)
場合分けが終わったら面積を出しましょう。もちろん、各議論の後に書いていても大丈夫です(3+3点)
犬:82点
感想「非常に体力が奪われる。疲れた。気づけばなるほどって思わされて歯がゆい思いをする。」
だそうです。そうですね。
1番とかもほかの解き方できそうですもんね。
犬、お疲れ様でした!
ちなみに、僕が解いた順番は、
1(15分)→3(10分)→4(15分)→5(20分)→6(20分)→2(35分)
です。参考にしてください。
1979年 東京大学 数学(理系) 前期

正方形の外側を、一次変換を施しましょう。2つの一次変換は両方とも平行四辺形になります。(3+3点)t≧0の範囲を考えますが、共通部分の面積を考えるので、0≦t<1と、t≧1で場合分けします。t≧1のときは、面積0になりますね。(3+3点)
グラフを書いて、最大値求めて終了です。最大値は微分して出しましょう。(グラフ4点+最大値4点)

平面で考え、xy座標に乗っけましょう。P原点とし、側面と円錐の高さのなす角θを用いて側面が
y=x/tanθと表せますね。この式のy≧0部分をy軸の周りにぐるぐるさせると、円錐ができます。球は円に見えているので、x^2+(y-t)^2=1とおきます。(t>0)
2つの式が接するので、連立したものの2次方程式が重解を持てばよいですね。(3点)
よって、tが求まります。1/sinθです。(2点)
接点は(x,y)=(cosθ,-sinθ+(1/sinθ))と求まります。
Kの体積は、円x^2+y^2=1の一部分をx軸周りにぐるぐるさせたものの体積に等しいと4みなせるので、求めましょう。(3点)
KとDの和を求め、Dの体積をθで表します。(2+3点)これが。球の体積の半分になればいいので、θに関する値を求めましょう。(3点)
Kの体積を求め終了です。(4点)

何個か、aを代入して、計算してみましょう。規則性が見えてくるはずです。
4で割った時のあまりで場合分けしてみましょう。もちろん、実験した内容を一般化してちゃんとこうなるって証明しましょう。(3+3+4+4点)
答えは4で割って1余らない数です。(6点)

xy座標に乗っけるのが楽だと思います。O原点、P(-1,0)にしちゃいます。
Qを(x+1)^2+y^2=4/3上にあると考え、(-1+2cosθ/√3,2sinθ/√3)と置きます。
RはQをP中心にπ/3回転させたところにあるので、1次変換を施します。(4点)
OQ^2+OR^2はθの関数になります。微分して、増減を考えましょう。
minθ,maxθがわかるので、min,maxが求まり終了です。(8+8点)
P,Q,Rがぐるぐる動かれるとこちらとしては厄介です。P置くと、QとRがある程度止まってくれるので、固定する考え方を持っておくといい感じです。

f(x)3次式なのでf(x)=ax^3+bx^2+cx+dとおく。原点を通るのと(B)より、f(x)=ax^3+x^2
になります。aをtで表しましょう。f(x)が確定します。(6点)
3次関数の対称性から上手にグラフを書きましょう。S(t)を積分で求めましょう。
値を飛ばして終了です。(6点+8点)

(1)相似比を考えて計算していきましょう。(8点)
(2)ベクトルの和を考えて、飛ばしましょう。(12点)
ざっくりしてますね笑 ごめんなさいw
2(20分)→3(10分)→4(15分)→5(10分)→1(25分)→6(30分)
今日はテストです。頑張ります笑
1978年 東京大学 数学(理系) 前期

xy座標に乗っけましょう。O原点、A1(0,1)、A2(-√3/2,1/2)、…っておきます。
P(0,p)(0<p<1)とおくと、PA1=1-pですね。こっから議論を始めます。
円Pの半径1-pですね。線分A3A6とPの距離を考えてみると、pの値が出ます。(3点)
OQとPA1とPCが等しくなります。OPとQA3とQCが等しくなります。
このことから平行四辺形が示せますね。(7点)
平行四辺形が示せたので、PC//OQ,OP//QC、∠A1PC=∠CQA3=2π/3となりますね。
これを利用して、勾玉型の面積を求めましょう(10点)

4次関数ですが、とりあえず、微分して増減考えて図を書きましょう。(2点)
場合分けは4つ生じます。一つ一つg(t)を考えましょう(4×4点)
グラフを書きましょう。(完答で2点)

(1)法線を出しましょう。(2点)
このtに関する3次方程式がただ1つの実数解をもつような(x,y)の範囲を考えればよいです。(1点)
y<0とy≧0で場合分けしましょう。(y<0:3点 y>0:3点)
図示して終了です。(3点)
(2)対称性を利用すると楽になりますね。63√2/135とかって出ます。(10点)

言われた通り帰納法を用いましょう。上三角行列なので、非常に楽だと思います。(8点)
an^2+bn^2を計算しましょう。汚くなりますが…(4点)
uとvを求めてみましょう。場合分けが生じます。(8点)

1/nがあるのでおやっと思いますが、普通に極限です。笑
∠ABCをθとでも置いて、極限飛ばした後に、余弦定理を使って、a,b,cで表していったほうがいいですね。
APk^2を余弦定理で表しまくります。難しくはないと思うので、丁寧にやりましょう。

(1)それぞれ面積を求めて不等式を考えましょう。簡単なので、これは取りたい。0<x≦2/3です。(6点)
(2)長くて嫌になりますね。
P以外の頂点をQ,Rとします。△PQR∊Mになるには、Q,Rは△ABCに含まれなければならないですよね。なぜならRが△PBD(PBを除く)にいるとき、PRとLの一部PDが交差しますからね。
場合分けが生じます。
1.Q,R∊AC 2.Q,R∊BC 3.Q,R一方がAC、他方がBC。逆も同様なのでこれだけで十分。(3×2点)
max△PQRは△PACか△PBCであることがわかります。(2点)
よってf(x)は(1)で求めた、h(x),g(x)の大きいほうです。(2点)
3(20分)→5(10分)→2(10分)→4(20分)→1(25分)→6(30分)
ただいま、絶賛テスト勉強中ですが、同じ学科の友達が泊りに来ているので、今1980年の問題を解いてくれているからそれに間に合わせるために書いています。笑
1977年 東京大学 数学(理系) 前期
おはようございます!(追記:1問目の途中でなぜか公開してましたすいませんw)

k≧0、k≦0で場合分けしましょう。絶対値の中身のグラフを先に書いて、x軸に関して折りたたんで、全部y≧0にもっていきましょう。
k≦0(2+3点)
k≧0(3+場合分け全部で5点)
M(k)のグラフが得られる(3点)ので、最小値を出しましょう。(4点)

ab,cosθ,sinθを、a1,a2,b1,b2や、それぞれで表します。(2点)
それぞれ1つずつから残り二つを示せば終了ですね(3×6点)
Qの加減乗除はQとなることを利用しましょう。

読むのもだるいかもしれないくらい面倒な問題です。一応頑張って書きます。
(ⅰ)
A⋂C\(A⋂C)⋂Bを図示しましょう。境界部分もちゃんと記述しましょう。(1点)
とりあえず、点Pを中止とした円の中で、領域A,B,Cに含まれるものの半径のMAXを、
それぞれr_A(P),r_B(P),r_C(P)とします。この中での最大のものがr(P)になりますよね。(2点)
今条件として、r_B(P)は考えなくていいですよ。P(a,b)として、bをfixします。
b<0、0≤a≤1-b/√3となりますね。(1点)
r_A(P),r_C(P)を、a,bで表します。(1点)
r(P)が最小となるのは、r_A(P)=r_C(P)となるときです。aをbで表せます。(1点)
minr(P)を出します。(1点)
maxr(P)は領域を考えたら存在しませんね。つまり上に有界でないです。
よって、答えはr(P)>-3+2√3です。(3点)
(ⅱ)
(ⅰ)の議論通り、Pがどこにいるかで場合分けしましょう。
Aのみ、Bのみ、Cのみ、A⋂C\(A⋂C)⋂B、A⋂C⋂B、B⋂C\(A⋂C)⋂B、
A⋂B\A⋂C⋂Bの7個です。(7点)
以上からr(P)の範囲を出しましょう。(3点)

π/2ずつ転がしましょう。2π動いたら、繰り返しますね。(4×2点)
V(a)を出します。(3点)
微分するのかと一瞬思うが、最小値なので、平方完成。(5点)
aの値と最小値を出して終了(4点)

(前半)成分比較しましょう。(8点)
(後半)t=tan(θ/2)とおくと、回転行列になることに気付けば終了です。(5点)
定石なのかな?でも行列はもう現課程にないからいっか…
θの範囲は決まっているので領域からその点だけ覗いてください(3+4点)
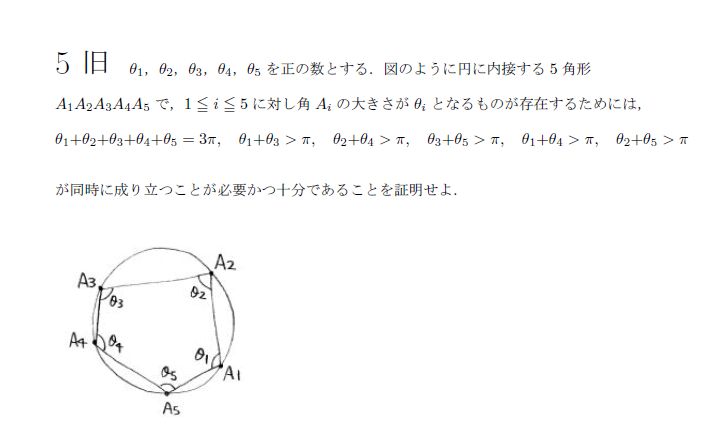
A1A3の線分を引きましょう。そうすることで、5つの式は証明できるので、必要条件は終了です(10点)
十分条件はθi<πを示せば、5角形は示せるし、後ろの5つの不等式が成り立つとき、円に内接するθiが存在することは明らかです。これで終了でいいと思います、(10点)

線形代数Ⅰで習ったので非常に簡単に感じられました。
(ⅰ)計算です。平面の方程式をax+by+cz+d=0とおくと、a,b,c,dに関する4つの条件式が得られます。連立しましょう。答えが得られます。(10点)
(ⅱ)parameterをt,sとして、l,mをそれぞれ表します。nを表したら、3式を連立して終了です。(10点)

f(x)をとりあえず、倍角の公式を利用してcosxの2次式にしましょう。(1点)
(ⅰ)cosx=tとおいて、議論していきましょう。微分して増減を考えます。
-1との大小を考えて場合分けして終了。(9点)
(ⅱ)今度はおいてはいけません。ある関数の変曲点の個数は何かで置換した関数と必ずしも一致するとは限らないからです。
2回微分します。(3点)
0<a≦1とa>1で考えましょう。(4点) 凹凸もちゃんと書いて終了です(3点)
2(15分)→4(10分)→5新(10分)→6新(10分)→6旧(10分)→1(20分)→5旧(25分)→3(over)
いや、第3問難しかったです…
1976年 東京大学 数学(理系) 前期
重くなってきました。頑張りましょう。僕が採点者だったらの点数配分なんで信憑性ないです!

Vを求めるまでは大丈夫でしょう。(3点)
r^2+l=c⇔ l=-r^2+c…★ (2点)
Vの中に含まれているlに代入しましょう。(2点)
微分して増減を考えましょう。(5点)ここで、★を考えましょう。lは負でない実数っていう条件をちゃんと使いましょう。0<r≤√cです!(2点)
極大値がその区間に入っているか否かで場合分けしましょう。(6点)

このままじゃ、論証が難しいです。
t=0での点Mの速度ベクトルを(1,0)とし、(ⅱ)に従ってMが動くとしましょう。
つまり、Pだと、(1,√3)の向きπ/3の方向に進んでいくのを、x軸に沿わせたらどうなるの?って考えています。
次にn1=(1,0),n2=(0,1)とおきましょう。
1秒間の全体移動距離を2,n1,n2,-n1,-n2方向の移動距離をa,b,c,dとします。
a+b+c+d=2です。…♪(3点)
c≧0,d≧0です。ただし、c≠0の時にはd>0となり得ません。(1点)
Mの最終到着点Nをベクトル表示すると、(a-c,b-d) です。(2点)
x=a-c,y=b-dとします。
x+yとx-yを♪を駆使しながら、範囲を見つけましょう。(3×2点)
これを図示します。(3点)
その図形をπ/3回転させれば終了です。(5点)

P(5+rcosθ,5+rsinθ)とし、Q(q1,q2)とでもします。PQの中点(9,0)です。
Qの座標をθで表します。(2点)
R(r1,r2)とおきます。回転を施す1次変換を思い出しましょう。Rの座標もθで表します。(2点)
QRの長さの2乗をrとθで表します(4点)
sinθとcosθの項は合成して範囲を見つけます。(合成2点+範囲2点)
根号の処理は最小値のほうは絶対値になります。(min3点、max2点)
f(r)=0⇔r=2√53ですね。(3点)

P(p,q)から接点までの距離を出します。(1点)
α(P)^2+β(P)^2+γ(P)^2をpとqの式で表します。(2点)
その値が99になるので(p-3)^2+q^2=27となりますね。(3点)
Pの領域の候補として、円(x-3)^2+y^2=27上にあることはわかりました。(2点)
とりあえずこの円はKとかとでもおきましょう。
KとA,B,Cの位置関係を調べに行きます。
B,Cは交差せず、Dの内部にいます。(2点+2点)
Aは交差します。つまり、その部分はAに接線引けませんよね。(2点)
よって、図示すると、左側のほうが円周の1/6が抉れた円になります。(3点)
つまり、円周の5/6の長さが求める答えです。(3点)

(ⅰ)f(x)を微分します。f'(x)=0になるxを求めます。0<x<1より、そのようなxは1つです。(2点)
増減表が得られます。その値αとし、f(α)の値を求めましょう。y=x^(-2)上を動きますよね。(2点)
もちろん範囲がありそうなにおいがするのでそれを探しに行きます。
αをtで微分すると単調減少しているので、αの範囲が決まります。(1点)
その下で、y座標も考えましょう。図示してどのように動くか記述して終了。(3点)
(ⅱ)αとtの大小関係を考えて場合分けしましょう。(3点+3点)
場合分けしたら2つの関数を図示しましょう。(4点)必ずつながるはずです。
どのように動くか記述しましょう。(2点)

非常に面倒ですね。とりあえず、P(cosθ,sinθ,0)とおきます。Pを通ってz軸に平行な直線と平面x-√3y+z=1の交点を、Q(cosθ,sinθ,z)とします。Qは平面上より
z=-cosθ+√3sinθ+1となります。(3点)
QがD内の点の時は、z≧0となりますね。(3点)
-π/3≤θ≤πでしょうか。(2点)
Dの面積はS=∫[-π/3→π](-cosθ+√3sinθ+1)dθ=4π/3+2√3(立式5点、答え7点)

dS/dtを求めます。そして、(1/x+1)(dx/dt)=1が出てきます。よって
log|x+1|=t+積分定数(3点) よって、x=e^(t+積分定数)となりますね。(3点)
t=0を代入すると、x=0ですので、C=0で、x=e^t-1ですね。(4点)
Sに代入しましょう。(3点)(完答7点)

(ⅰ)2つの行列を持ってきましょう。Cayley-Hamilton th.で、A^2を次数下げします。(4点)
積を計算して、属すること示して終了。(3点)
(ⅱ)Gから1つもってきて、detを計算します。(2点)
この値が0とならなければいいですよね。(2点+元の行列の値が0とならない条件も書いて1点)
a=0と仮定すると矛盾するのでa≠0を導きます(2点)
判別式<0で、条件が出てきます(2点)図示して終了(3点)

(ⅰ)4個の相異なる実根をもつので(x-α)(x-β)(x-γ)(x-δ)と表せますね。(1点)
場合分けします。
k=0のとき、f(x)=0は4個の実根をもちますね。(1点)
k≠0のとき、g(x)=f(x)+kf'(x)とでもおきます。
αを代入しても、β、γ、δを代入しても0じゃないです。
g(x)=0の両辺を(x-α)(x-β)(x-γ)(x-δ)で割ります。
1+k(1/(x-α)+1/(x-β)+1/(x-γ)+1/(x-δ))=0となります。
kでくくった中身のグラフを考えると、3つ実根を持ちます。-∞に飛ばすと0に行きます。
これをk倍に拡大(縮小)し、y軸方向へ1平行移動します。これで、1つ実根が増えます。(4点)
以上より、いずれの場合も4個。(3点)
(ⅱ)
極値3つあります。p,q,r(p<q<r)とでも置きます。
f''(x)=0を満たす2解はp<x<q,q<x<rにExistしますね。
f(x)=0,f''(x)=0が相異なる共有点をもつので、x=β、γです。
f(x)=のKKKよりα+β+γ+δ=-a(3次以上の解と係数の関係使いこなせると便利。)
f''(x)=0のKKKより、β+γ=-a/2
2式よりα+δ=β+γが得られます。(ここまでで5点)
f(x)をうまく2つ平方完成しましょう。(3点)
よってx=(α+δ)/2に関して対称が示せます。(カッコ内はβ+γでもOK)(完答で3点)
1(15分)→2(20分)→3新(10分)→3旧(20分)→4(20分)→6新(10分)→5旧(5分)→5新(10分)
→6旧(35分)
2時間25分です!適当に点数予想しちゃってるけど怒られないかな…
