1975年 東京大学 数学(理系) 前期

両端がある線分2つを選び場合分けしました。それぞれのPQの長さを考えてあげると、
どの位置にいるのかわかり
ます。

まずx=1とでも代入しましょう。2^k-1=2^m
k≧2の時は不適、k=1のときm=0、k=0のとき不適、よって、k,mが確定します。
後は係数比較しましょう。∀xに対して成り立たないといけないので、最初の行為は必要条件だと思います。逆にこの時~みたいな感じで最後に記述しましょう。

直線と放物線が接するから,-ax^2+bx=-x+4が重解を持ちますね。するとaをbで表せます。代入して重解をbで表します。重解は(0,4)の間にいるので、bの範囲が決まります。
面積を求めて、bの範囲の下で微分して増減を考えると出てきます。
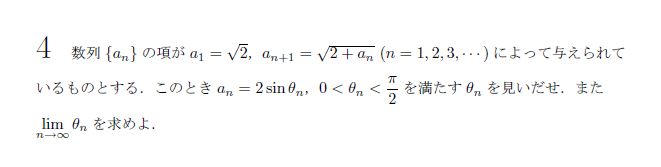
明らかに両辺が正なので、2乗しましょう。sinの2乗と1乗があって、中身も違うので、まずは2乗を1乗に(倍角公式をうまく使います。)そこから、cosとsinの関係を利用して、sin1次の式の関係が出てきて、漸化式が作れます。これを解いて、飛ばしましょう。

(ⅰ)v1を求めます。後は、a^3/8^n倍ってことに気づけば大丈夫です。
はじめからa/2^nとかで計算すると容量オーバーになります。やめましょう。
(ⅱ)(ⅰ)が出ていればできます。等比数列の和の公式は覚えておきましょう。

(ⅰ)①n回目でx個→次でも変わらない
②n回目でx+1個→次でx個
③n回目でx-1個→次でx個
互いに排反なので題意が示せます。
(ⅱ)(ⅰ)を利用するほかありません。少し面倒かもしれません。
(ⅲ)(ⅱ)で計算間違えていなければ3に飛ぶでしょう。
2(5分)⇒3(10分)⇒4(10分)⇒6(20分)⇒5(20分)⇒1(30分)
前年度に比べたら易化している感じはしますが、徐々に難しくなっていきますね。
1974年 東京大学 数学(理系) 前期

十進法です。普通の数です。mod10(10で割った余り)で分類することを思いつきます。
(1) 1,2,3,4,5,6,7,8,9,10それぞれ2乗した時の数を見れば終わりです。
(2) n^5-nの1の位が0つまりn^5-nは10の倍数であることを証明します。帰納法です。
連続するn個の整数はn!の倍数であることは覚えておきましょう。
(3)n^100=(n^20)^5であるから、(2)より、n^100の1の位はn^20の1の位
動揺にn^20の1の位はn^4の1の位。(1)の値を2乗すれば終了。
両端をA,Bとし、(a,a^2),(b,b^2)(a<b)とでも置いて、中点の座標も出しましょう。
a+b,abの値が中点の座標に出てくるので、判別式≧0の条件があることを忘れないようにしましょう。さらっと書いているけど結構重要です。
計算ぐちゃぐちゃするけどがんばりましょう。今回は相加相乗平均が見えるので使っちゃいましょう。難しいです。
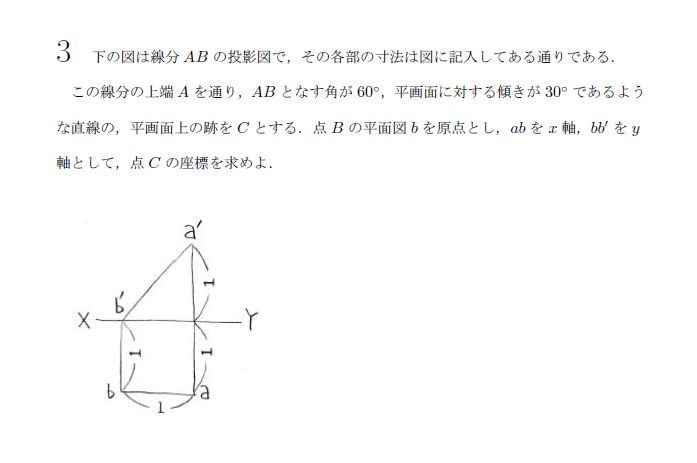
文字が統一されていないので解く側としてはわかりませんね。
条件よりB(0,1,0),A(1,2,0),A'(1,0,0)となり、AB=√2です。
△AA'Cについて考えるとACが求まります。Cの座標を適当に置いて(xz平面にあることを考慮しながら)式を2つ考えると答えが求まります。4乗根出てきます。

3)、1)と2)、4)の順に考えました。f'(0),g'(0)は2次方程式の2解になります。KKKを使って終了です。

cycloidの問題です。一度解いてみればこの手の問題は解決できると思います。
(1)(2)はすぐにできますね。
(3)弧長の公式を思い出しましょう。

(1)Aが優勝する確率を考える。3連勝するか、3試合までA 2勝1敗→次にAが勝つ
または、4試合までA2勝2敗→次にAが勝つのいずれかです。
Pをpの式で表せたら、P+Q=1、p-q=1をつかって、(P-Q)-(p-q)の増減を議論していきましょう。
(2)微分して増減を考えましょう。答えはぐちゃぐちゃしてます。
(3)長いですね。Nは3,4,5です。4は面倒に見えてくると思うので余事象から出していきましょう。
期待値を出したらその値を微分して増減を考えましょう。
1(10分)⇒3(20分)⇒4(10分)⇒5(10分)⇒2(30分)⇒6(35分)
このsetは非常に疲れると思います。2と6は体力勝負ですね。
少し雑談します。一応二十歳超えているのですが、やっておけばよかったって後悔するものが2つあります。
1.ヴァイオリン
2.本を読む習慣
ピアノを習わせてもらっていたので1は何も文句言えません。なんでやりたいかというと、四月は君の嘘の影響です笑
2.は本当に心の底から思っています。だから、4月から活字に少しずつ触れていっていますが…本当に悔やまれる。特に目上の人や、年上の人と話すとき自分の教養の無さに呆れます。といって自分の周りの大学生見ても活字読んでいる人は少ないですけど苦笑
先週、傑作と言われているイニシエーション・ラブを読みました。感動したけど、自分が一度されたことがあるので、心のショックが大きいです。一週間たった今も正直落ち込んでいます。
だから、適当な理由をつけて先週の授業を一緒に受けている子に渡しました←
きっと読むよって後でLINE来たけど笑
1973年 東京大学 数学(理系) 前期
1973素数ですよ!!!!!!
じゃ、いきまーす。(素数ネタは数学科としての責務だと感じています)
これは難しいですよね。Nを(a/2,0,√3 a/2)としても一般性失いません。おきましょう。また、Pの動く円を含む平面をxy平面にしちゃいましょう。これも一般性を失いません。
こう考えるといくらか楽になりませんか?
Nの接平面とxy平面の交線をL、直線Lと点Pの描く円との交点をA,Bとしましょう。
NからPが見えるのはLによって分けられる円周のうち、Oと反対側の弧AB上に点Pがあるときです。A,Bの座標を、図と、三平方から出しましょう。(もちろん、平面で見てください)Aだけ求めればいいです。Bは対称性で何とかなりますからね。∠AOBを出しましょう。その値を速さπ/12で割れば8秒って出てきます。
NPのmaxはA,Bにいるときで、minはP(4a,0,0)にいるときですよね。

1番見て飛ばそうと思って2番を見て、涙目になる…受験生の視点からすると焦る組み合わせだと思います。
x_1,x_2,...,x_nのうち1,2の個数をそれぞれa,b,とすると、
f1=a+2b,f2=a+4bですね。これから,a,bをf1とf2を用いて表せます。
fkは帰納的にa+2^k・bです。a,bを代入して終了です。
気づけばすぐですね。

1次式なので非常に簡単です。
(ⅰ)1つ1つの場合分け丁寧にやりましょう。
(ⅱ)ⅰで求めた答えを横軸a,縦軸V(a)として図示してみましょう。minは容易に求まります。

Sの中心を原点に、それぞれの辺を軸に平行になるように座標を導入します。
対称性で第1象限で議論しましょう。(x-1)(y-1)≧1/2が出てきますね。
よって、対称性より、Pの存在範囲は簡単に出ますね。
面積は第1象限に着目してその面積を4倍すればいいです。

(2)の左辺と右辺の交点を求めて、グラフを考えます。特に増減調べなくても不等式の証明を使えば、大まかな2つの曲線の位置関係がわかりますね。
f(t)を表したら、あとは微分しましょう。積分関数の微分ですね。x/(1+x^2)=g(x)みたいに置くと計算が楽に。

とても簡単です。最初の条件でy=ax^2+xと書けます。aをu,vで表して傾きを出しましょう。
6(5分)⇒2(5分)⇒3(10分)⇒5(10分)⇒4(15分)⇒1(30分)
1に時間かけすぎちゃいました汗
簡単な問題は簡単だけど、1とかで焦ると解けなくなるんですよね。怖い。
1972年 東京大学 数学(理系) 前期
今日はまだ書きますよ。明日はあさってのテスト勉強(暗記ゲー)が始まるので…

対称性より、xz平面をみます。△OPBに着目しましょう。∠APBをθとでも置いて、出てきたものをsinでもcosでもtanでもいいから条件を出しましょう。xy平面をみてみると対称性をもった図が現れますね。積分せずとも幾何的に解きましょう。

難しいと思います。まず、BとB'はkに関して対称なのでベクトルbとベクトルb'の和はkと平行になり、ベクトルc(太文字はベクトルって知らなかったらこれ混乱するでしょ…)と垂直です。CとC'についても同様な議論を行います。2つの式が出てきます。ベクトルcの大きさが√mって出てきます。∠BAC=θとおいて、ベクトルbとベクトルcの内積=それぞれの大きさをかけ、cosθをかけた値になるので、ベクトルbの大きさ1をヒントにして、m=1,2,3が得られます。3つの場合を全部出して終了です。お疲れ様です。

Fibonacciみたいな関係が出てきそうですよね。この図は。
図形と数列みたいなものが絡んでいるときは、かならず、n番目とその前後の関係を図示してから議論始めましょう。
三平方の定理3つ使ってr_nの漸化式が得られます。これを解くと、Rとnの式としてr_nが出てきます。あとはn^2r_nを計算して無限に飛ばしましょう。

k=f(x)/g(x) (x≠±1,-4)として、グラフを書いて、直線y=kとy=f(x)/g(x)のグラフの交点を求めましょう。実根の個数と対応します。分数型のグラフを考えるときは、y=pの漸近線以外にもほかの漸近線があることを忘れないでくださいね。

積分方程式っていう名前でしたっけ…忘れました。
とりあえず、u(x)をxについて2回微分して(1)を使いましょう。
f(x)は一次関数だからy=ax+bとかでも置きましょう。
a,bの値にかかわらず成り立てばいいので、恒等式を二つ解きましょう。
(2)の条件も忘れずに考えると、h(x)はとても簡単なものになります。
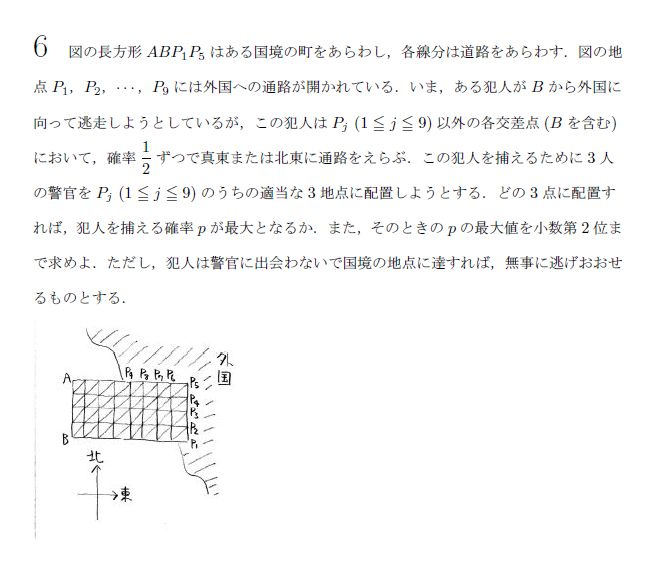
面倒な問題ですね。小数第2位まで求めろって小学生的ですね。
僕はP1~P9まで場合分けさせてもらいました。
一番確率が多い、3つの部分にポリスを置きます。4,6,7かな。
確率は50%超えます。逃げ果せるなんて仰々しい文章受験数学で初めて見ましたよ笑
1(10分)⇒4(10分)⇒5(10分)⇒6(20分)⇒3(15分)⇒2(30分)
まだ解いたストックかなりあるので、書ける書ける…笑
1971年 東京大学 数学(理系) 前期

普通にx^2+y^2を求めてから微分してもいいですが、yをsinで表してみると(t-π/6)になってめちゃくちゃ楽になります。

(1)an+1について解きます。ak+1-ak(k∊N)が0以上になることはわかりますが、akが1か否かで話が変わってきます。もちろん1になったら全部イコールになっちゃうので、1だと仮定して矛盾を導きましょう。すぐに矛盾します。帰納的にan≠1が言えます。
よって最初にかいたak+1-ak≧0より、帰納的にan-an-1>0が言えるので、証明終了。
(2)(前半)(1)と同じように考えましょう。x<2なので、すぐ見えてくるでしょう。
(後半)εが出てきてるのでε-N論法みたいなのを考えちゃいます。笑
ak≤1-εなので、ε≤1-akで、ak+1-ak≧ε^2/2がk∊Nで言えますね。
これを縦に並べて辺々足しましょう。an-1-1≧nε^2/2が言えます。
で、an<1は前半で言っているので、題意が示せますね。
久しぶりに長々と書いてしまいました。論証は書きたくなっちゃいます。

f(x)をax^n+bx^n-1+...的な感じで置くのはやめましょう。
最小値を実際に出さなくていいので、a,bの条件が出るようにしてあげます。
(f(x)-ax-b)^2を展開します。そして、上の2つの条件を代入します。
∫[0→1]f(x)^2dx+ a^2/3 +b^2 -6a +ab -4b って出てきます。
まず、aについて平方完成します。残った項はbの式として見て平方完成します。
先にbの値が出てきて、代入して整理するとaの値も出てきます。

このfn(x)の正体はeのMaclaurin展開です。前半は微分しましょう。それだけ。
後半は誘導通り数学的帰納法を用いましょう。注意するところは、仮定でn=2k-1でただ1つの実根をもち、n=2kで実根をもたないので、最初はn=1,2で成立を確認、
n=2k+1,2k+2のとき成り立つことを示しましょう。記述量は非常に多いので、頑張りましょう。

集合と論理の円周の期末テストに、偏角として(cos2πk/n,sin2πk/n)として、k/nの部分がQなので、Nと濃度が等しいから題意が成立する的な(ざっくりしてますねごめんなさい)問題があったので、最初の一文を読んで思わず笑いがこみあげました。
まぁ、計算していけばわかるのですが、snの部分に1/nあるし、λpでぶっ飛ばさせてるので区分求積法です。
|ベクトルPQk|^2を計算します。kの値を0~n-1代入したものを足しましょう。

グーチョキパーじゃないあたり、この問題の古さを感じますね。面白い笑
場合分けです。k-1回目まであいこで、k回目で1人勝ち。またはk-1回目のどこか1回で1人負け、k回目で勝負が決まる。これらは排反です。足しましょう。
1(5分)⇒3(5分)⇒5(5分)⇒6(5分)⇒4(20分)⇒2(25分)
演習量を積んでいない子にとってはheavyだと思いますが、難しくはないです。頑張りましょう。
1970年 東京大学 数学(理系) 前期

de Moivreの定理より、a^n=cos(nπ)/3+isin(nπ)/3と表せます。もし、de Moivreの定理を知らなかったら、帰納法でいきましょう。
(1)nπ/3は、周期6でぐるぐる回りますね。場合分けしましょう。答えは6個です。
(2)これも場合分け6個しましょう。出てくる答えは2つです。

(1)3回目に必ず±1,±3にいるので、4回目には絶対いませんね。
0、±2、±4の確率をそれぞれ出しましょう。
(2)全事象は2^n通りですね。頑張りましょう。

物理やっている人はできて当然です。物理やってない人は、頑張りましょう。
速度を積分すれば距離になりますね。逆にいうと距離を微分すると速度になります。(接線の傾き)これを駆使して、答えを出しましょう。

物理要素がかなり強いです。1970年のsetは。
水槽の右側をy軸ととる座標を導入しましょう。t秒後の噴流の座標をparameter表示します。
(1)床の上⇔y=0です。
(2)xの混合の中身を平方完成しましょう。
(3)噴流の軌跡をtを消して出します。hについての2次方程式が出るので、それが、0<h<aの範囲で解をもつような(x,y)の集合が噴流の通過範囲です。2通りの場合分けが生じます。
1(20分)⇒2(15分)⇒3(20分)⇒4(20分)
意外と時間かかりました。4問だけだったのに。
物理選択の人はちゃんと完答しましょう。
1962-65年 東京大学 数学(文系) 前期
1962

線を引いてその部分の面積を求めて、その個数分求める、中学生的解法で解けますね。
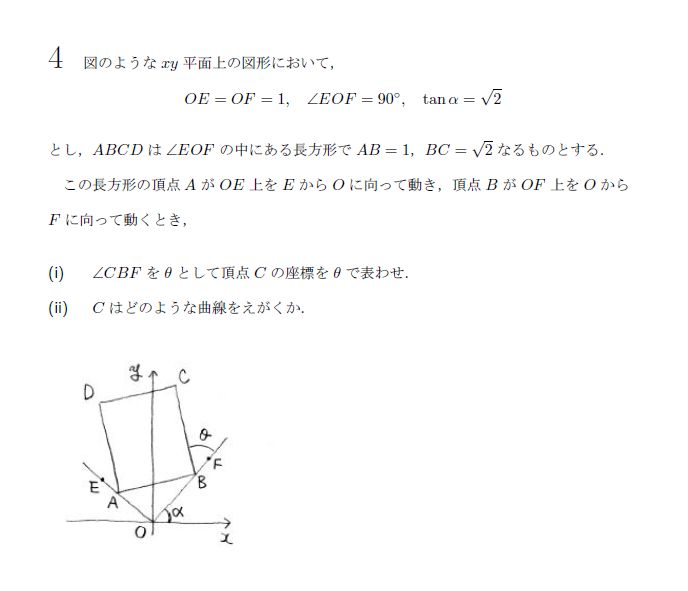
(ⅰ)Cの座標はθとαで表せますね。tanα=√2からαを消しましょう。
(ⅱ)行列の知識を用いていいのなら、回転行列を表すものが導き出せますよね。y座標だけ1/2がつくのには注意しましょう。
1963

(1)微分して増減を考え、5に近づけたとき、無限に飛ばしたときetc.グラフを書くときのオーソドックスな解法を使いましょう。
(2)(1)のグラフより得られますね。
(3)(1)のグラフを考察しましょう。

toのときのx,yを表し、微分して、f'(t0),g'(t0)を出しましょう。条件より、x,yの変化率の2乗の和はものすごく簡単になりますよ。
αの式が出れば、あとは最も小さくするようなαの値ですね。微分は不必要ですよ。
1964
この年はほとんど理系と共通で1問だけでした。

Pは(t,at^3+bt^2+ct+d)とかにしましょう。Qを出します。
あとはAQ^2,AP^2,を落ち着いて出して、0と無限に飛ばしましょう。それぞれ定数になります。
1965
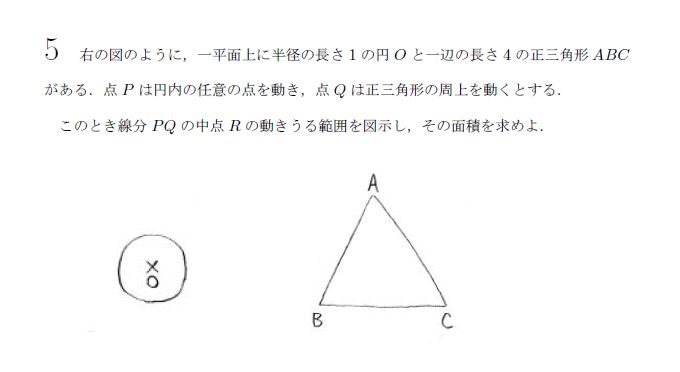
河合塾で浪人していた時、この種の問題に出会った覚えがあります。懐かしい。
受験数学はこういう時、武器になりますよ。
2点ぐるぐる回るのは嫌です。1個fixします。
Pをとりあえず、原点にfixしましょうか。
OA,OB,OCの中点をそれぞれ、X,Y,Zとかと置くと、Rの軌跡は、一辺の長さ2の正三角形XYZの周上となりますね。中点連結定理からです。
Pをmoveします。
Rの軌跡は半径1/2の円になるので、円の中心は、正三角形XYZの周上を動きます。
よっておにぎり型の軌跡の概形が得られます。面積を求めて終了です。
とりあえず、ここまでにしておきます。文系はしばらくはいいかな笑
理系を解いていきます。
