阪大挑戦枠に挑戦する①

挑戦しました。とりあえず１番を見たときにこれは似たような解法を用いる問題に出会ったことを思い出しました。後期の線形代数ⅱ演習のプリントの難しい問題のうちの１つにありました。

それは、ある条件が４つあって、そのもとで、ある式が内積となるかどうかという問題でした。

これは、自分は整数までしか解けず、教授のところに質問しに行ったら、「じゃあ黒板でやっていこう」と言われ、マンツーマンで黒板に貼り付けにされた思い出があります。叱られ、叱られ、とても精神的にダメージをもらいましたが、その問題と出会ったときに思い出しました。１１月頭のことだったと思います。あー懐かしい。

あれ？横になっちゃった笑

こんな感じです。実数を有理数、整数、自然数っていう風に分けて、

自然数スタートで実数まで導こうっていう考え方です。まぁその考え方自体はすぐに思いつき、その当時も同じように考えたのですが…。こっちの問題はできたのでまぁいいでしょうか。

でも、やっぱりうれしいんです。

うまく説明できないですねこの感じ。

たとえるなら、

みなさんどっかで嗅いだにおいを別の場所で嗅ぐと、懐かしい感じになるじゃないですか？あの感じです←　その感覚に浸っていてとてもふわふわしています。

問題に対しても一度やったことのある骨折りの問題に似たものを見ると懐かしさ、嬉しさを感じます。

1986年 東京大学 数学（理系） 前期

ごちゃごちゃ動くので、とりあえずCをfixしましょう。次はAでもBでもいいですが、

Cを固定したところとAの場所で場合分けして、Aをfixして、Bがどの位置で面積が最大になるか考えましょう。

円に変換したほうがいいでしょうか。

円に変換しなかったとき議論を進めていって最終的に面積を求める積分の時に置換積分をしますが、その置換は円に変換する作業と相当していると感じました。

y軸方向に2倍拡大して議論をしましょう。こっちは、幾何的に解けます。面積が求まったら、ちゃんとy軸方向に1/2倍縮小することを忘れないようにしましょう。

何度も言いますが、円に変換しなくてもできます。計算量はほんのちょっと増えますが、それでも多くないです。簡単です。

(1)外積は当時の課程にあったのでしょうか。とりあえず、外積です。外積を求めるのがわからなかったら、ABCのそれぞれのベクトルと垂直をなすものを探しましょう。

(2)戸惑うとしたら、ここでしょうか。

 

まぁ、ざっくり書くとこんな感じですが、空間図形の定石通り、断面を考えます。すると、平面Sの法線ベクトルとlのなす角は一定であることがわかります。

長さ1という条件、角、n0を用いると、x-y=±1/3という式が出てきます。

場合分けしましょう。すると最大値(1+√17)/6、最小値0が出てきます。

最小値0は感覚的にもわかりますよね。

(1)aを固定してもいいですし、uかvを固定してもいいです。どちらにしても、同じ答えが求まりますね。

(2)僕は、(1)の誘導を全く使いませんでした笑　本来は使った方がいいのかもしれませんね。線形計画法とか一文字固定とかいろいろ(1)の(u,v)平面を用いる考え方はありますが…計算量は僕の考え方が一番軽いと思います。

解の公式から議論をして、a=0.9,b=3.3,c=4.5の時が最大値を与え、a=1.1,b=2.7,c=5.4の時に最小値を与えることを証明しました。

笑

これはクローズアップ問題ですね。重箱の隅をつついた問題ですね笑

これがもし本番だったら時間オーバーでした。僕は1時間以上使わせてもらいました。

 (1)この断面を考えていくと、とりあえず、Lは求まりますね。次は水面線の中点を通り、底面に平行な平面で切ります。そうすると、aとbが求まると思います。少々考えにくいと思います。

(2) (1)とπabh/3を用いるとmの式が出てきます。mについて頑張って解きましょう。答えは(3-2^(5/3))/5でしょうか。

1(15分)→2(20分)→3(25分)→4(15分)→6(25分)→5(over)

非常に疲れました。 

受験生お疲れ様でした。新受験生、これからもっと頑張っていきましょう。

お疲れ様でした。２日間の間気力、体力ともにかなり消耗したと思います。ゆっくり休んでください。後期ある人は踏ん張りどころです。頑張りましょう。

アクセス数が600越えまして…ありがとうございます。しかし、なぜアクセス数が増えるのだろうと思っていたら、検索エンジンで東大数学　～年とかで調べると恥ずかしながら出てくるようになっていましたね苦笑

あくまでも、周りがやっているから僕もブログやるかって感じで始めたものがちょっとずつアクセス数増えるのは本当にうれしいです…笑

多分、今の年まで戻ったら、今までの記事を校正して、TeXに直したりしようと思いますので、見にくかったり、ざっくりしているものは今はスルーしてください笑

管理人本人の現在ですが、

①塾講師

塾講師が今週から始まり、小６、中３の算数、数学の演習系統の授業を担当することになりました。演習系統は本科の授業の理解の補強や、発展的思考を育てていくものと解釈しているので、楽しいです。今日、明日は代講で少し遠いところの校舎に行くことになっています。がんばります。

②自動車学校

こちらはまったりやっています。ひっかけ問題とか…苦手です。頑張ります。

③大学数学

解析入門を紐解いていってます。微分方程式です。狭義のRiccatiの微分方程式にかなり頭使いましたが、先に進んでいます。いまだもやもやしています。難しいです。

微分方程式終わったら…微積分を始めたいと思います。Green’s th.やdivergence th.やStokes’ th.ですね。こちらは、受験数学のネタが尽きてきたり、僕の備忘録として綴っていこうかなって思っています。

1985年 東京大学 数学（理系） 前期

今回、交点のx座標は求まりません。これ自体を文字で置くのは演習でいろいろやっているかとは思います。aを残すか、自分で置いた文字を残すか自由ですが、どちらかを消去して、最大値を求めましょう。簡単です。

問題文通りに角θとかで表してみましょう。三角方程式の解の個数の問題は一度は触れたことがあると思いますが、一応個数は注意しましょう。昔、河合塾で習った先生の俳句で「消える文字　範囲残せば　消えてよし」ってありました。うまいですね。これは覚えておいて損はないです。

対称性に気付き、さらに底面の選び方でぐっと難易度が変わると思います。

Q,Rの座標を求めます。QRの中点をMとすると、△OPMを底面とみなすと非常に楽です。

(1)A^nは予想して、帰納法に持ち込みましょう。三角行列のn乗は規則性がすぐ見えます。１次変換を施し、問題文通り手を動かしましょう。

(2)代入して微分してみるとわかりますが、極小値をとる(1.21)^nの候補として√2が出てきます。安易に1.414だから1のほうが近いんじゃね？とか思わないようにしましょう。答えは2です。

問題文を読み解くのは難しいですね。実験しましょう。pn=p0^(n+1)はすぐに予想できます。帰納法で証明しましょう。期待値っぽい形をしてますが、p0が|p0|<1となることは、示せるので、convergeするときの無限等比級数の和の公式を思い出しましょう。p0=1/2と出てしまいます。あとは、計算しましょう。答えは1ですｗ

非回転体ですが、とりあえず、球を動かす前にぶつ切りにしましょう。

(1)ですが(2)を見据えてz=tで計算をしておきましょう。それに0を代入すればokです。

計算量は多いです。頑張りましょう。

1(10分)→2(15分)→3(15分)→4(20分)→5(10分)→6(20分)

計算量は多いですけど、それにしても80年代入ってからの中ではこのsetは易しめだったと思います。

明日から塾講師のバイトが始まるんです。相手は小学生ですけど笑

6問目の切り口と同じ図が小6のテキストに載ってて笑いましたね。

やはり計算力をつけるには小学生から鍛えておいた方がいいのでしょうか。もちろん完璧にはならなくていいんですけどね…

1984年 東京大学 数学（理系） 前期

空間座標の方程式を知らないときついです。

Cの周はCを含む平面と中心(0,1/√2,1/√2)、半径1の球面との交わりです。

Cを含む平面は、y-z=0と考えられます。この平面は(1,0,0)と(0,1,1)に平行であるから、(0,1,-1)を法線ベクトルとしてもつからです。また、今回の球面は

x^2+(y-1/√2)^2+(z-1/√2)=1と書けます。

ⅰ)とりあえず、Sの輪郭上の点をQ(a,b,0)とします。直線PQ上のある点Rは

(ta,tb,2√2(1-t))と表せますね。(t∊R)

この点Rがy-z=0上にあるときは、tをa,bで表せますね。これでRの座標がすべてa,bで表せますね。

これを球面の式に代入しましょう。整理すると、円の式が出てきます。

ⅱ)

幾何的に解きましょう。大きい円錐と小さい円錐を見つけたら終了。

２つの曲線が接していて、共通の接線が引けることに注目しましょう。

三平方の定理や直交する条件を使いましょう。

難しくはないと思います。

難しいですね…。頭の柔らかさ？がキーポイントだと思います。

ⅰ)Σ[k=2→n]akfk(x)と表されることは、理解できると思います。

a0=a1=0となれば終了です。

ポイントとしてはfk(x)が(x-a)^kで割り切れるとはf(a)=f'(a)=0=…f^(k)(a)=0が成り立つこと。TeXの表し方で表せるようになったらこの部分はわかりやすくしようと思うので…。これを使いましょう。

ⅱ)　ⅰ)を使いましょう。ⅰ）の条件に加えてg''(1)=0が成り立ちますね。

回転させる前に軸に平行なものでぶった切ります。切り口はドーナッツの形になりますね。その面積を求めて、積分しましょう。

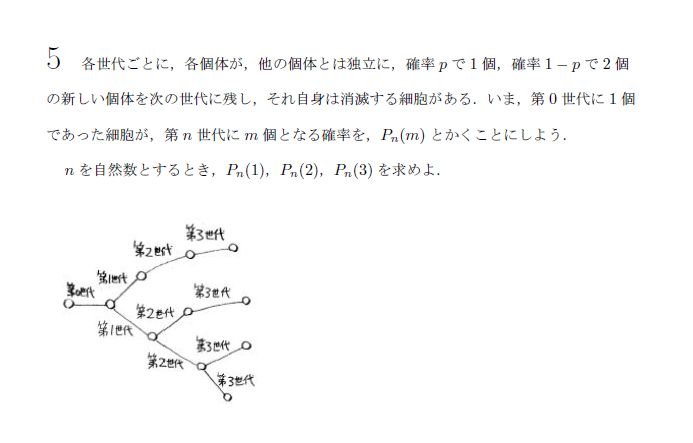
方針はすぐに立つと思いますが、計算量は非常に多いと思います。直接確率を出すか、確率漸化式の方法がありますが、後者のほうがほんのちょっと楽かと。

計算量で思い出しましたが、数学科の専門授業でそれぞれの分野に対し演習の授業がうちの大学にはあります。（これだけで特定されてしまう可能性も否めませんが笑）

各担当の教授によってその演習の方式はガラッと変わりますが、ある分野の演習の担当として数学科の中で一番厳しいと言われている先生に僕の学年は後期に当たっていました。黒板の前で発表の形式ですが、非常に寧な方で、少しでも計算過程を省くと容赦なく突っ込んでくるのでプレッシャーとの戦いでした。（僕は３回発表しましたが笑）頭の中で計算してしまうので、何回か厳しめに指導されて少し心が折れましたが、毎週の宿題を解いているうちに計算力は非常に上がったと思っています。東大の問題を俯瞰しても、計算がややこしいものでも、嫌がることはなくなったのでとても感謝しています。笑　高校の時にこういう先生に出会いたかったｗ

閑話休題、とりあえず、推移図を書きましょう。個体数が減少することはないことをうまく考えましょう。

Pn(1),Pn(2)は計算量としてはそんなに多くないです。

また、Pn(2)、Pn(3)は、場合分けが生じます。頑張りましょう。

これは逃げ出したくなる問題なんじゃないかなって思います。Descartesの困難は分割せよ。って言われても、今回は分割したところで…って思う人も多いと思います。

受験で分割の作業をしても文意を掴めなかった場合は、Einsteinの次の言葉を覚えておきましょう。「物事はすべて、できるだけ単純にすべきだ。」

Descartesと似ていますね。とりあえずわかりやすくすればいいんです。もちろん自分の解釈を馬鹿正直に答案用紙に書くのではなくて、あくまでも自分の理解のためにすればいいのです。変な解釈をすればそれは間違いになってしまいますが…

DとEを連立してみると(x,y)=(2,4)が出てきます。これは鍵です。

D、E、Uを表せたら、解の配置問題として解くのがいいですね。KKKが楽でしょうか。

2(10分)→3(10分)→4(10分)→1(25分)→6(20分)→5(40分)

最近更新してないのにもブログを見てくださってる方がちらほらいてくれて感謝です。ありがとうございます。ちょっと多忙な時期なので…

1983年 東京大学 数学（理系） 前期

12日に友達が泊りに来てマリカとマリテオールして、13日は学科の飲み会で14日はバイトの二次選考の流れでブログを書く気力おきませんでした笑

大学の勉強のほうは、微分方程式を1から独学を始めました。先輩にテキスト借りて早く終わらせるためにとりあえず頑張ります。

難しく考えずに、素直に問題文に従っていきます。

後、これは必要条件と十分条件に分けていくのが定石だと思います。一気に必要十分を考えるのが難しいからです。

(1)より、任意の形ですが、特殊な三角形を考えてみたいと思います。正三角形です。

(2)より、とりあえず、A(1,√3)、A'(-2,2√3)と置きましょう。原点は自分自身に移るので、

Bを(2,0)と置いて△OABが1次変換によってどこに行くか考えましょう。

必要条件として、2つの行列が出てきます。なぜならBの移動先の候補が二つあるからです。

十分条件を確認すると確かに題意を満たしているので大丈夫です。

二進法に気付けばほとんど自明ですね。一応帰納法です。nの値を代入していけばわかります。二進法に気付けないときは、いっきに二つの事柄を証明します。anと(1)と(2)の内容です。

題意に従って、文字を置いていきましょう。

円C上の点Pは(cosθ,sinθ,0)とおけ、(0≤θ<2π)

直線l上の点QはA(a,0,0)をとおり、xy平面とのなす角が45°なのでQ(a,t,t)とおけますね。(t∊R)

最短距離をaとθで表して、最小値を求めましょう。

1文字固定をしましょう。aの大きさ（つまりAの位置)で場合分けが生じます。

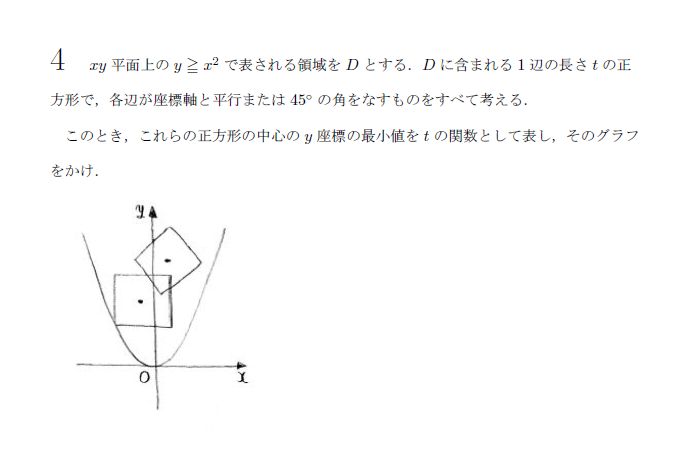
場合分けをするのは問題文に従えばすぐわかりますね。

(ア)正方形の各辺が各座標軸と平行なとき、

最小値ってことは、正方形の下側の頂点2つがy=x^2に乗ってればいいですね。

下側の頂点が(±t/2,t^2/4)と表せるので、このとき、中心y座標のminが出ますね。

(イ)45°のとき、

これも２つ場合分けが生じますね。

下側の頂点が原点と一致するか、左右の頂点がy=x^2上にあるかどうかですね。

y=x^2とy=±xの交点を考えると、この２通りが同時に起こる正方形の一辺の長さは√2ですね。

その値より、大きいとき、小さいときで、考えればいいですね。

全部の場合分けが終わったらグラフを書きましょう。

minなので、そのグラフを考えたとき、yの値が大きくないほうを選べば勝ちです。

対称面の切り口を考えるのが定石ですね。長さを変数で置いてもいいですが、対称面の角度を変数にとる方が楽な気がします。

これは難しいと思います。2番か6番がこの年の踏ん張りどころでしょうか。

とりあえずy=aでぶった切ります。切り口はaを消去すると、x^2+z^2=-y+3/4です。

さて、次にHを考えますが、y=xとしてもいいでしょう。/////

そんで、y=xに平行な平面y=x+b(b≧0)で切った断面をxz平面に正射影します。

その図形は(x+1/2)^2+z^2=1-bですね。1-b≧0⇔b≦1より、この図形の面積はπ(1-b)ですね。

y=x+bとxz平面は45°の角をなすから、正射影前の図形はπ(1-b)/cos45°=√2π(1-b)です。

y=x+bとy=x+b+Δbの距離はΔb/√2であるから、体積は

∫[0→1]√2π(1-b)・db√2=π/2　が答えです。

この問題が難しいと思うポイントは

①回転体が不完全で、回転軸に垂直で切っても無理

②正射影が思いついたとして、元に戻してあげたとしても、その微小体積を足し合わせるときに厚みがΔyとかでないこと。

いわゆる斜回転体の先駆けでしょう。

別解はいくらでもあります。/////までは思いつかないといけないと思いますが…

3(10分)→4(15分)→1(15分)→5(20分)→2(30分)→6(30分)

1982年 東京大学 数学（理系） 前期

以下、太文字をベクトルとします。ベクトルOPをpとします。

題意よりAp=p⇔(A-E)p=0ですね。ここで、A-Eが逆行列をもたないと仮定しましょう。つまりdet(A-E)≠0と仮定します。そうするとp=0となりますが、点Pは原点以外に矛盾しますね。

よってdet(A-E)=0です。(a-1)(d-1)-bc=0(2点)

ここで、lは、sx+ty=1(s,t∊R\｛0｝)とおけるのは大丈夫でしょうか。s=1/m,t=1/n的に置くとx切片がm、y切片がnの直線になりますね。原点は通りません。(3点)

この直線上の点A(x,y)を一次変換で移しましょう。A'(ax+by,cx+dy)ですね。こいつが元の直線にいるにはsx+ty=1を満たす(x,y)に対してs(ax+by)+t(cx+dy)=1を満たす(s,t)が存在すればいいです。（s,tって置いたのは分数を嫌ったからです）(4点)

(a-1)s+ct=0とbs+(d-1)t=0が条件ですね。この2式の係数を並べた行列の行列式は0になっています。最初のほうに戻って確認してください。

よって、(a-1,s)と(b,d-1)は一次従属です。(3点)適当にr(≠0)とp,q∊Rを用いて

(a-1,b)=pr、(c,d-1)=qrとおけますね。よって、２式に戻して考えると、ps+qt=0を満たせばよいですね。(3点)

p≠0とすると、(s,t)=(-q,p)、p=0の時は、(s,t)=(1,0)とすれば満たされます。(4点)

以上より示されました。ポイントはlの置き方とかでしょうか。

正四面体の辺に接するんです。辺ですよ、辺。イメージし難いんじゃないでしょうか。面とかがあるからいけないんでしょうね。とっちゃってみましょう。

その辺にある爪楊枝6本もってきてくっつけると、空洞ですよね？そんな感じです。

解法は2つありますよね。対称面で切る方法(定石)と正四面体と立方体の関係です。

 体積は、結局回転体の体積として扱いますけど、対称面は見つけてもらうとして、正四面体と立方体の関係を考えます。

立方体の頂点から4点をうまくもってくると、正四面体が得られます。確かめてください。そうすると、立方体の球面Sの内接球っていうのは、各面の中心で接しているから、Tの各辺は立方体の対角線となってますよね。よって、立方体の1辺の長さは2なので、答えは2√2です。前半終了です。(10点)

後半は、積分です。

Tの1つの面の内接円の半径は、√(2/3)です。これは頂点から底面におろした垂線の足は底面の重心になることからですね。(2点)

ぼこっと出ている題意の体積部分までの球の中心からの距離は、√3/3です。計算してみてください。これが4つあります。積分して終了です。(8点)

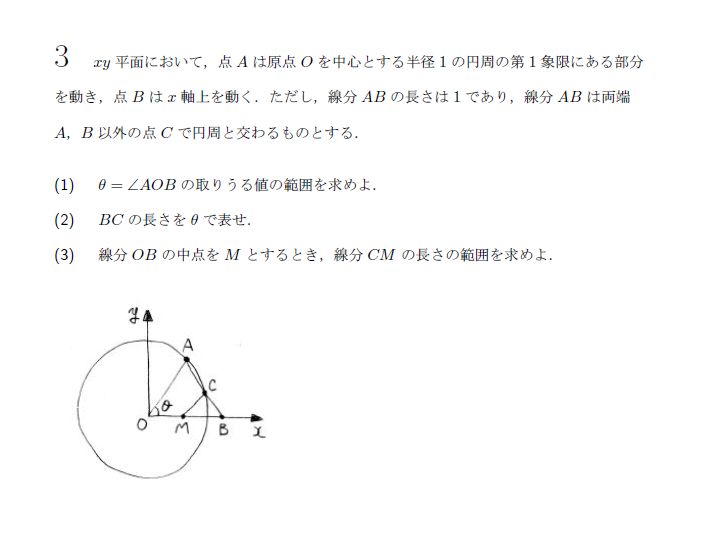
(1)ABと円がA,B以外の交点をもてばいいですね。(5点)

(2)計算です。△OABは二等辺ですから、解けますね。(5点)

(3)△BCMに着目しましょう。余弦が使えます。

CMの２乗を計算できたら、グラフ等を利用して範囲を出しましょう。(10点)

これは物理やっている人はできますね。波動的な。

x方向、y方向に分けて議論しましょう。答えはV^2ですね。

非回転体の体積ですね。概形は１式が竹を斧でぶった切って出てくる、ぐわんとなったやつです笑　ごめんなさいまったく概形考えなくていいですよ笑

どの文字で切るかは、わかりますか。xかyです。式に出てきた回数または高次のもので切りたいからです。とりあえずy=tで切りたいですね。(0≤t≤1)

切り口は台形ですね。面積を求めます。

これを0から1まで積分して終了です。

(1)計算しましょう。(2点)

(2)推移図を考えましょう。(6点)

(3)pn+qn+rn=1が成り立つことを気づくと(2)の結果から瞬殺です。(12点)

3(15分)→5(10分)→6(15分)→4(25分)→2(20分)→1(15分)

書いているときに思いました。重いです笑

だから、まぁ簡単だなってやつはものすごく簡略してます。別に適当にしてるわけじゃないですよ汗